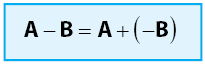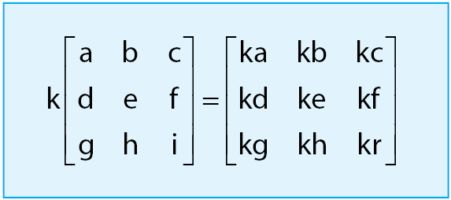FUNGSI KUADRAT
A. PENGERTIAN FUNGSI KUADRAT
Fungsi kuadrat
adalah suatu fungsi yang pangkat variabel tertingginya adalah dua.
Bentuk umum fungsi kuadrat :
f(x) = ax2 + bx + c atau y = ax2
+ bx + c
|
dengan
a ≠ 0 dan a,b,c
R
B.
GRAFIK FUNGSI KUADRAT
Grafik fungsi kuadrat berupa
kurva yang berbentuk parabola.
1. Jika a > 0 (a positif) maka
parabola/grafiknya terbuka ke atas.
2. Jika a < 0 (a negatif) maka
parabola/grafiknya terbuka ke bawah
Istilah – istilah pada
fungsi kuadrat :
Dari
gambar tersebut diperoleh :
·
x
1 dan x
2 adalah titik potong kurva dengan sumbu
x
·
c adalah titik potong kurva dengan sumbu y
·
P adalah titik puncak
·
x = d adalah sumbu simetri
C. TITIK POTONG TERHADAP SUMBU – SUMBU KOORDINAT
Terdiri atas 2 macam yaitu :
1. Titik potong
terhadap sumbu x
Agar grafik
fungsi kuadrat y = ax2 + bx + c memotong sumbu x, maka
nilai y haruslah sama dengan nol (0).
Nilai x yang menyebabkan fungsi y = f(x) = 0 disebut pembuat nol
fungsi.
y = 0 → ax2 + bx + c = 0
(x – x1) (x – x2)
= 0
Koordinat titik potongnya (x1,0) dan (x2,0)
2. Titik potong
terhadap sumbu y
Agar grafik
fungsi kuadrat y = ax2 + bx + c memotong sumbu y, maka nilai x
haruslah sama dengan nol (0).
x = 0 → y = a (0)2 + b(0) + c
y = c
koordinat titik potongnya
(0,c)
D. TITIK PUNCAK / TITIK BALIK DAN SUMBU SIMETRI
Bentuk y = ax2
+ bx + c, mempunyai :
* Sumbu simetri
(penyebab ekstrim) ialah garis yang membagi parabola secara simetris.
Rumus untuk sumbu simetris :
* Nilai ekstrim ialah nilai tertinggi (maksimum)
atau nilai terendah (minimum) yang dicapai oleh suatu fungsi. Nilai ekstrim maksimum terjadi jika parabola
terbuka ke bawah atau jika a < 0 sedangkan nilai ekstrim minimum terjadi
jika parabola terbuka ke atas atau jika a > 0 .
Rumus untuk nilai ekstrim :
atau
dengan memasukkan nilai sumbu simetri ke persamaan kuadrat.
* Titik puncak
parabola
– jika a > 0 atau parabola terbuka ke
atas, maka titik puncak adalah titik balik minimum
– jika a < 0 atau parabola terbuka ke
bawah, maka titik puncak adalah titik balik maksimum.
Rumus untuk titik puncak :
E. MENGGAMBAR GRAFIK FUNGSI KUADRAT
Langkah – langkah
menggambar grafik fungsi kuadrat :
- Menentukan koordinat titik potong
terhadap sumbu x dan sumbu y
- Menentukan persamaan sumbu simetri
- Menentukan nilai ekstrim
- Menentukan titik puncak
- Melukis kurva parabola melalui titik
– titik yang telah ditentukan
Contoh 1 :
1. Gambarlah grafik fungsi kuadrat y
= x2 + 2x – 3 !
Jawab :
a = 1 , b = 2 , c = – 3
a = 1 → a > 0, maka parabola terbuka ke
atas
* Titik potong terhadap sumbu x
(pembuat nol fungsi)
Jika y = 0 → x2 + 2x – 3 = 0
(x – 1) (x +
3) = 0
x = 1 ,
x = –3
didapat
koordinat titik potong (1,0) dan (–3,0)
* Titik potong terhadap sumbu y
Jika x = 0 → y = 02
+ 2.0 – 3
y =
–3
didapat koordinat titik potong (0, –3)
* Persamaan sumbu
simetri :
x = –1
* Nilai ekstrim:
y =
atau y =
(–1)2 + 2(–1) –3 =1 – 2 – 3= –4
didapat nilai minimum y = –4
* Titik puncaknya
adalah (–1, –4)
2. Gambarlah grafik fungsi kuadrat y
= –x2 + 6x – 5 !
y = –x2 +6x – 5 , maka
a = – 1 → a < 0, maka parabola terbuka
ke bawah
* Titik potong terhadap sumbu x (pembuat nol fungsi)
Jika y = 0 → –x2 + 6x – 5 = 0
x = 1
didapat koordinat titik potong (1,0) dan
(5,0)
* Titik potong terhadap sumbu y
Jika x = 0 → y = 02
+ 6.0 – 5
y =
–5
didapat koordinat titik potong (0, –5)
* Persamaan sumbu
simetri :
x =
atau x =
x = 3
* Nilai ekstrim:
y =
atau y = –(3)2 + 6(3) –5=–9 +18–5 = 4
didapat nilai maksimum y = 4
* Titik puncaknya
adalah (3,4)
Menggambar grafik
fungsi kuadrat jika diketahui daerah asal (domain) fungsi.
Contoh 2 :
1. Gambarlah grafik fungsi kuadrat y = x2 + 2x – 3 dengan domain
!
Jawab :
y = x2 + 2x – 3
Df
=
|
X
|
–4
|
–3
|
–2
|
–1
|
0
|
1
|
2
|
|
x2
2x
–3
|
16
–8
–3
|
9
–6
–3
|
4
–4
–3
|
1
–2
–3
|
0
0
–3
|
1
2
–3
|
4
4
–3
|
|
Y
|
5
|
0
|
–3
|
–4
|
–3
|
0
|
5
|
|
(x,y)
|
(–4,5)
|
(–3,0)
|
(–2,–3)
|
(–1,–4)
|
(0, –3)
|
(1,0)
|
(2,5)
|
Didapat Rf
=
2. Gambarlah grafik fungsi kuadrat y = –x2
+ 6x – 5 dengan domain
!
|
x
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
|
–x2
6x
–5
|
0
0
–5
|
–1
6
–5
|
–4
12
–5
|
–9
18
–5
|
–16
24
–5
|
–25
30
–5
|
–36
36
–5
|
|
Y
|
–5
|
0
|
3
|
4
|
3
|
0
|
|
|
(x,y)
|
(0, –5)
|
(1,0)
|
(2,3)
|
(3,4)
|
(4,3)
|
(5,0)
|
(6, –5)
|
Didapat Rf =
LATIHAN 1 :
1.
Gambarlah
grafik fungsi kuadrat dari persamaan di bawah ini :
a.
y = x2
+ 2x – 24
b.
y =
–x2 + 6x – 9
c.
y =
2x2 – 11x +14
d.
y =
4x – x2
e.
y = x2
– 2x + 1
2.
Gambarlah grafik fungsi kuadrat dari persamaan di bawah ini dan tentukan
wilayah hasil fungsinya !
a. y
= x2 + 4x – 5 dengan daerah asal
b. y = –x2
– 2x + 3 dengan daerah asal
c. y = x2
– 1 dengan daerah asal
d. y = x2
– 2x + 3 dengan daerah asal
e. y = –x2
+ 4x + 8 dengan daerah asal
F. KEDUDUKAN GRAFIK FUNGSI
KUADRAT TERHADAP SUMBU X
Kedudukan grafik fungsi
kuadrat y = ax
2 + bx + c terhadap sumbu x secara keseluruhan ada 6
kemungkinan.
Keenam kemungkinan
kedudukan itu ditentukan oleh tanda – tanda dari “a” (koefisien x
2)
dan tanda – tanda dari diskriminan
Perhatikan tabel di bawah ini :
|
Tanda a dan D
|
Bentuk Kurva
|
Kurva y = ax2
+ bx + c terhadap sumbu x
|
Jenis titik
balik kurva
|
|
a > 0
(a positif)
|
D > 0
|
|
Memotong sumbu
x di dua titik yang berbeda.
x1 ≠ x2
|
minimum
|
|
D = 0
|
|
Menyinggung sumbu x di satu titik.
x1
= x2
|
Minimum
|
|
D < 0
|
|
Tidak memotong sumbu x (definit positif)
|
Minimum
|
|
a < 0
( a negatif)
|
D > 0
|
|
Memotong sumbu x di dua titik yang berbeda.
x1 ≠
x2
|
Maksimum
|
|
D = 0
|
|
Menyinggung sumbu x di satu titik.
x1
= x2
|
Maksimum
|
|
D < 0
|
|
Tidak memotong sumbu x (definit negatif)
|
Maksimum
|
Contoh 3 :
1. Diketahui fungsi kuadrat f ditentukan dengan
rumus f(x) = 2x2 – 4x – p .
Tentukan batas nilai p agar grafik fungsi f memotong sumbu x di dua
titik yang berlainan !
Jawab :
f(x) = 2x2
– 4x – p → a = 2, b = –4, c = –p
a = 2 → a > 0
syarat agar grafik
fungsi f memotong sumbu x di dua titik yang berlainan adalah :
D > 0
b2 – 4ac
> 0
(–4)2 –
4 . 2 . (–p) > 0
16 + 8p > 0
8p > –16
p >
p > –2
2. Diketahui fungsi kuadrat f ditentukan dengan
rumus f(x) = mx2 – 2mx + ( ½ m + 1).
Tentukan nilai m agar grafik fungsi f menyinggung sumbu x !
Jawab :
f(x) = mx2
– 2mx + ( ½ m + 1) → a = m, b = –2m, c = ½ m + 1
Syarat agar grafik
f menyinggung sumbu x adalah:
m > 0 atau m < 0
D = 0
b2 – 4ac =0
(–2m)2 – 4. m ( ½ m +
1) =0
4m2 – 2m2 – 4m = 0
2m2 – 4m = 0
2m ( m – 2) = 0
2m = 0 m
– 2 = 0
m = 0 m
= 2
yang memenuhi m = 2, kareana a > 0 atau
a < 0.
3. Tentukan nilai p, agar bentuk f(x) = (p – 1)x2
– 2px + (p – 2) definit negatif !
Jawab :
f(x) = (p – 1)x2
– 2px + (p – 2) → a = (p – 1), b = –2p,
c = (p – 2)
Syarat definit
negatif adalah a < 0 dan D < 0
* a < 0 → p – 1
< 0
P < 1
* D < 0 Degan
menghubungkan syarat 1 dan syarat 2
b2 -
4ac < 0 Lihat
gambar di bawah ini :
(–2p)2 – 4(p – 1)(p – 2)
< 0
4p2 – 4(p2 – 2p
– p + 2) < 0
4p2
– 4p2 + 12p – 8 < 0
12p < 8
p <
maka
nilai p yang memenuhi adalah p <
p
<
G. MENENTUKAN PERSAMAAN FUNGSI KUADRAT
Untuk menentukan persamaan fungsi kuadrat
jika diketahui grafik fungsi kuadratnya dapat dilakukan dengan cara :
1. Jika
grafik fungsi kuadrat memotong sumbu x di titik (x1 ,0) dan (x2
,0) serta melalui sebuah titik tertentu, maka rumusnya :
2.
Jika
grafik fungsi kuadrat melalui titik puncak (xp,yp) serta
melalui sebuah titik tertentu, maka rumusnya :
3.
Jika
grafik fungsi kuadrat melalui titik – titik (x1,y1), (x2,y2)
dan (x3,y3), maka rumusnya :
Contoh 4 :
Tentukan persamaan fungsi
kuadrat pada grafik (parabola) di bawah ini !
Jawab :
1. Grafik memotong sumbu x di titik (–1, 0) dan (4,0) dan melalui titik
(0,2)
y = a (x – x1)(x – x2) Masukkan nilai a :
2 = a (0 – (–1)) (0 – 4) y = a (x – x1)(x – x2)
2 = a (1)(–4)
y = –½ (x – (–1)) (x – 4)
2 = – 4 a y
= –½ (x + 1) (x – 4)
a =
= –
y =
–½ (x2 – 4x + x – 4)
y
= –½ (x2 – 3x – 4)
y
= –½ x2 +
x + 2
Jadi persamaan fungsi kuadratnya
adalah : y = –
x2 +
x + 2
2. Grafik melalui titik puncak ( –1
, –4) dan melalui titik ( –3 ,0)
( –1 ,–4) → xp= –1 , yp=
–4 masukkan nilai
a :
(–3,0) → x = –3 , y = 0 y = a (x – xp)2
+ yp
y = a (x – xp)2 + yp y
= 1 ( x – (–1))2 + (–4)
0 = a (–3 – (–1))2 + (–4) y = 1 ( x + 1)2
– 4
0 = a (–3 + 1)2 – 4 y = 1 ( x2
+ 2x + 1) – 4
0 = a (–2)2 – 4 y = x2
+ 2x + 1 – 4
0 = a.4 – 4 y
= x2 + 2x – 3
4 =
4a
a =
= 1 Jadi
persamaan fungsi kuadratnya adalah : y = x2 + 2x – 3
3. Grafik melalui titik – titik
(0,0), (1,6) dan (4,0)
(0 , 0) →
y = ax2 + bx +
c eliminasi
persamaan 2 dan 3
0 = a .02 + b .0 + c a + b = 6 .4 4a
+ 4b = 24
0 = c ............(1) 16a + 4b = 0 .1 16a + 4b =
0 –
(1,6) → y = ax2 + bx + c````````` -
12a = 24
6 = a (1)2 + b(1) + c a = – 2
6 = a + b + c substitusi nilai a =
–2 ke persamaan 2
6 = a + b + 0 6 = a + b
6 = a + b ……(2)
6 = –2 + b
(4,0)
→ y = ax2 + bx + c
8 = b
0 = a(4)2 + b(4) + c substitusi
nilai a =–2, b = 8 dan c =0 ke rumus :
0 = 16a + 4b + 0 y = ax2 + bx + c
0 = 16a + 4b…..(3) y = –2x2 + 8x + 0
y = –2x2 + 8x
Jadi persamaan fungsi kuadrat adalah :
y = –2x2 + 8x
LATIHAN 2:
1. Tentukan persamaan grafik fungsi kuadrat dari
kurva di bawah ini !
2. Sebuah
fungsi kuadrat mempunyai nilai maksimum 4 yang dicapai pada x = 1. Fungsi kuadrat itu bernilai 0 untuk x =
3. Tentukan persamaan fungsi kuadrat
tersebut !
3. Fungsi
kuadrat f melalui titik – titik A (0 ,–6) , B (–1, 0) dan C (1,–10)
Tentukanlah
:
a).
Persamaan fungsi kuadrat tersebut!
b).
Titik – titik potongnya dengan sumbu x !
c).
Titik puncak / titik balik grafik fungsi f !
LATIHAN FUNGSI KUADRAT
- Koordinat titik balik dari fungsi kuadrat f(x) = 4x2
– 5x + 1 adalah ........
A.
C.
E.
B.
D.
(UN Thn. 2005/2006)
- Grafik dari fungsi f(x) = –x2
+ 4x – 6 akan simetris terhadap garis ......
A. x = 3 B. x = 2 C. x = –2 D. x = –3 E.
x = –4
(EBTANAS Thn. 2000/2001)
- Nilai a agar grafik fungsi y = (a –
1)x2 – 2ax + (a – 3) selalu berada di bawah sumbu x (definit
negatif) adalah .......
A. a = 1 B. a > 1 C. a < 1
D. a >
E. a <
(EBTANAS Thn. 2000/2001)
- Perhatikan grafik fungsi kuadrat di bawah
ini!
Persamaan dari grafik di
samping adalah................
A.
y = x2 –2x + 3
C.
y =
–x2 + 3x + 2
E.
y = x2
+ 3x – 2
- Grafik fungsi y = 4x2 – 8x
– 21, memotong sumbu x, sumbu y dan mempunyai titik balik P berturut –
turut adalah ……
A. x =
, x =
, y = 21 , P (1,25) D. x =
, x =
, y = –21 ,
P (1,–25)
B. x =
, x =
, y = 21 , P (–1,25) E. x =
, x =
, y= –21 , P(–1,–25)
C. x =
, x =
, y = –21 , P (1, –25)
(UN Thn. 2002/2003)
-
Grafik fungsi kuadrat f(x) = 2x2 + 11x – 6 adalah .....
- Titik balik grafik dari fungsi
kuadrat y = –3x2 + 6x + 2 adalah ........
A. (–⅓ , 0) B.(2,0) C.(0,2) D. (5,1) E.
(1,5)
- Sumbu simetri parabola y = kx2
+ (k – 1)x + 1 adalah x = 3. Nilai
k adalah ......
-
Persamaan dari grafik fungsi
kuadrat di samping adalah.......
A. y = x2 – 4 D. y = –x2 – 4x
B.
y = x2 – 4x E. y = x2
+ 4x
10. Persamaan
fungsi kuadrat yang sesuai dengan gambar grafik di samping adalah ……..
A.
y = –2x2 + x D.
y = 2x2 + x
B.
y = ½ x2 – x E.
y = x2 – 2 x
(UN Thn 2004/2005)
- Grafik fungsi kuadrat yang mempunyai
titik balik (2,1) dan melalui titik (4,5) persamaannya adalah ……
A. y = x2 – 2x +1 C.
y = x2 + 2x – 7 E.
y = x2 – 4x +5
B. y = x2 +4x +5 D.
y = x2 – 4x –5
(EBTANAS Thn. 1996/1997)
- Diketahui fungsi kuadrat f(x) = –2x2
+ 4x + 3 dengan daerah asal
. Daerah hasil
fungsi f adalah ……….
A.
C.
E.
B.
D.
(EBTANAS Thn 1997/1998)
- Fungsi kuadrat yang mempunyai nilai
minimum 2 untuk x = 1 dan mempunyai nilai 3 untuk x = 2 adalah ……
A. y = x2 – 2x +1 C.
y = x2 +2x –1 E.
y = x2 +2x +3
B. y = x2 – 2x +3 D.
y = x2 +2x +1
(UMPTN Thn 1996)
- Grafik fungsi kuadrat yang
persamaannya adalah y = 6 + px – 5x2 memotong sumbu x. Salah satu titik potongnya adalah
(–2,0), maka p samadengan ……….
A. –13 B. –7 C. 6 D. 7 E.13
(EBTANAS Thn 1991/1992)
- Sebuah peluru ditembakkan vertikal dengan
persamaan lintasan h(t) = 150t – 5t2. Tinggi maksimum peluru
adalah..............
A. 925 m C.
1.025 m E. 1.225 m
B. 1.015 m D.
1.125 m
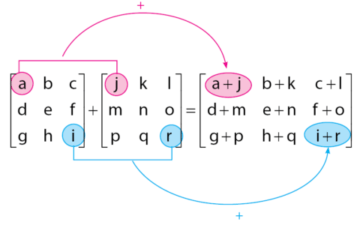
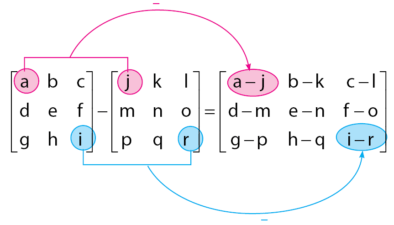
 , di mana elemen-elemen matriks
, di mana elemen-elemen matriks  merupakan lawan dari elemen-elemen matriks A. Secara ringkas, sifat operasi penjumlahan matriks dapat dilihat pada gambar di bawah.
merupakan lawan dari elemen-elemen matriks A. Secara ringkas, sifat operasi penjumlahan matriks dapat dilihat pada gambar di bawah.